 |
Getting Started |  |
| How Parsers Work |
| Main | |
|
|
Latest News |
|
|
Getting Started |
|
|
Screen Shots |
|
|
Download |
|
|
Documentation |
|
|
Contributors |
|
|
Contact |
| About GOLD | |
|
|
How It Works |
|
|
FAQ |
|
|
Why Use GOLD? |
|
|
Comparison |
|
|
Revision History |
|
|
Freeware License |
|
|
More ... |
![]()
Deterministic Finite Automata
A Deterministic Finite Automaton is used to perform lexical analysis for the parser.
 As the name implies, deterministic finite automata are
deterministic. This means that from any given state there is only one path for any given
input. In other words, there is no ambiguity in state transition. It is also complete
which means there is one path from any given input. It is finite; meaning there is a fixed
and known number of states and transitions between states. Finally, it is an automaton.
The transition from state to state is completely determined by the input. The algorithm
merely follows the correct branches based on the information provided. As the name implies, deterministic finite automata are
deterministic. This means that from any given state there is only one path for any given
input. In other words, there is no ambiguity in state transition. It is also complete
which means there is one path from any given input. It is finite; meaning there is a fixed
and known number of states and transitions between states. Finally, it is an automaton.
The transition from state to state is completely determined by the input. The algorithm
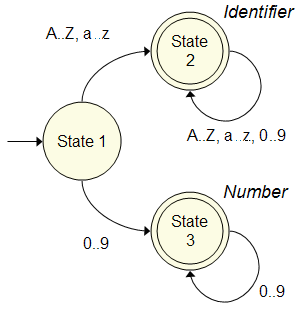
merely follows the correct branches based on the information provided. A DFA is commonly represented with a graph. The term "graph" is used quite loosely by other scientific fields. Often, it is refers to a plotted mathematical function or graphical representation of data. In computer science terms, however, a "graph" is simply a collection of nodes connected by edges. The figure to the right is a simple Deterministic Finite Automata that recognizes common identifiers and numbers. For instance, assume that the input contains the text "gold". From State 1 (the initial state), the DFA moves to State 2 when the "g" is read. For the next three characters, "o", "l" and "d", the DFA continues to loop to State 2. By design, the tokenizer attempts to match the longest series of characters possible before accepting a token. For example: if the tokenizer is reading the characters "count" from the source, it can match the first character "c" as an identifier. It would not be prudent for the tokenizer to report five separate identifiers: "c", "o", "u", "n" and "t". |
LALR
The LALR algorithm is used to perform syntactic analysis for the parser..
 Like Deterministic Finite Automata, the LALR algorithm is a
simple state transition graph. Each state represents a different stage the system can be
in as it parses a string. Like Deterministic Finite Automata, the LALR algorithm is a
simple state transition graph. Each state represents a different stage the system can be
in as it parses a string. Each state represents a point in the parse process where a number of tokens have been read from the source and rules are in different states of completion. Each production in a state of completion is called a "configuration" and each state is really a configuration set. For each token received from the. lexer, the LR algorithm can take four different actions: Shift, Reduce, Accept and Goto. For each state, the LR algorithm checks the next token on the input queue against all tokens that expected at that stage of the parse. If the token is expected, it is "shifted". This action represents moving the cursor past the current token. The token is removed form the input queue and pushed onto the parse stack. A reduce is performed when a rule is complete and ready to be replaced by the single nonterminal it represents. Essentially, the tokens that are part of the rule's handle - the right-hand side of the definition - are popped from the parse stack and replaced by the rule's nonterminal. When a rule is reduced, the algorithm jumps to (gotos) the appropriate state representing the reduced nonterminal. This simulates the shifting of a nonterminal in the LR state machine. Finally, when the start symbol (the nonterminal used to represent the entire grammar) is reduced, the input is both complete and correct. At this point, parsing terminates. |